{1}/ Pergunta difícil
Por que o primeiro algarismo 2 de 222 vale duzentas unidades, o segundo vale vinte, e o terceiro vale só duas?
Quanto à pergunta, existem três tipos de gente no mundo: o tipo A, o B, o C. (Excluindo gente que não tem a mínima ideia.)
O tipo A é um tipo comum, pois uma pessoa tipo A é uma pessoa comum, se a missão do momento é atinar com explicações matemáticas. Gente desse tipo, quando se arrisca e dá uma resposta à pergunta, entra num circuito fechado: usa o próprio fato que está tentando explicar como explicação do fato que está tentando explicar.
— Por que o primeiro 2 está na casa das centenas.
— Sim, OK, mas por que a primeira casa é a casa das centenas?
— Porque o 100, veja bem o 100, o algarismo 1 está na casa das centenas e ele vale 100. Então o algarismo 2, se está nas centenas, deve valer 200.
O diálogo vai mais ou menos nessa linha, e demora bastante a sair disso.
O tipo B é menos comum. Gente desse tipo conhece uma explicação técnica.
— O primeiro algarismo 2 de 222 vale duzentos porque você deve multiplicar todo número na casa das centenas por 100. Se você escrevesse 47 na casa das centenas, por exemplo se escrevesse 47-2-2, estaria falando de 47 × 100, mais 2 × 10, mais 2 × 1, então estaria falando de 4.722.
Esse tipo resolve problemas aritméticos básicos com desenvoltura, mas, se o interlocutor insiste em saber por que deve multiplicar os algarismos na casa das centenas por 100, o tipo B não consegue produzir uma explicação apenas com ideias mais simples que a ideia que está tentando explicar. Entre professores de matemática, há uma porcentagem que é do tipo B.
Dizer isso não significa desmerecer nenhum professor. Quase todos os brasileiros tomaram contato com essas ideias quando eram crianças, e depois passaram a ser tratados como se as conhecessem bem. É natural que dominem tais ideias razoavelmente, do ponto de vista técnico, mas que não tenham a capacidade de explicá-las a partir de termos mais simples, que até crianças possam compreender. E o ciclo se repete.
Finalmente, existe o tipo C, que é mais raro. É gente capaz de produzir uma explicação simples, ainda que longa, e que não recorre ao próprio fato que está tentando explicar à guisa de explicação do fato que está tentando explicar.
O propósito deste texto é ajudá-lo a se transformar numa pessoa tipo C.
{2}/ Um entre infinitos
Numa faculdade de matemática, um estudante (vamos chamá-lo de C2h) entra no centro acadêmico, bate palmas e, quando todos olham para ele, proclama:
— Não existe o sistema numérico posicional decimal!
Alguns riem, um amassa uma bolinha de papel e taca na direção do proclamador, e outro retruca:
— É claro que não: todo sistema posicional decimal é um sistema posicional decimal. Um entre muitos: um entre infinitos!
C2h já ouviu muita gente dizer que o sistema numérico usado no Brasil é “o sistema numérico posicional decimal”, com o artigo definido “o”. Talvez até tenha lido algo assim, sem que o autor tenha feito nenhuma ressalva.
É quase verdade, mas falta uma informação importante para justificar o artigo definido “o”.
O sistema numérico brasileiro é decimal, pois C2h usa dez símbolos (algarismos) para representar cada número. E ele é posicional, pois o valor que C2h atribui a cada algarismo varia conforme a posição que o algarismo ocupa no numeral. (Em 22, o primeiro 2 vale vinte unidades, e o segundo 2 vale só duas unidades.) Mas, para dizer o nome e o sobrenome desse sistema, C2h deve dizer: “Sistema numérico posicional decimal hindu-arábico.”
— Não existe o sistema numérico posicional decimal — ele deveria ter proclamado, se quisesse evitar uma bolinha de papel —, mas sim o sistema numérico posicional decimal hindu-arábico!
Isso porque C2h usa não os dez algarismos A, B, C, D, E, F, G, H, I, J, sempre nessa ordem, nem os dez algarismos α, β, γ, δ, ε, ζ, η, θ, ι, κ, sempre nessa ordem, mas, em vez disso, usa os dez algarismos 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, sempre nessa ordem, isto é, do algarismo de menor valor ao algarismo de maior valor. Para resumir uma história longa e complicada, tais algarismos foram criados por intelectuais árabes e indianos (talvez com base em ideias vindas da China), e espalhados pela Europa do século 13 pelo matemático italiano Fibonacci, entre outros. É por isso que C2h, quando escreve num papel o inteiro 236, está usando o sistema posicional decimal hindu-arábico. Só existe um sistema assim, e essa é talvez a única criação humana usada do mesmo jeito em quase todas as cidades do mundo.
{3}/ Ambiguidades de notação
C2h deve dizer que o primeiro 2 de 22 vale vinte ou que o primeiro 2 de 22 vale dois? Deve contar os algarismos da esquerda para a direita ou da direita para a esquerda?
Quando conversa sobre um número específico, como 6.743, C2h costuma seguir uma convenção venerável: conta os algarismos da esquerda para a direita: o primeiro algarismo é 6; o último, 3. Essa contagem reflete o modo como quase toda gente escreve os números: primeiro escreve o algarismo mais significativo e, por último, o menos significativo. Quando C2h conversa sobre dois números, como 6.743 e 82, aí existe a possibilidade de confusão, pois o primeiro algarismo de 6.743 está na posição dos milhares, e o primeiro de 82, na posição das dezenas. O jeito é recorrer a artifícios como 0.082 ou a expressões como “o algarismo na posição das unidades”, “o algarismo na posição das centenas”, etc. C2h já aprendeu que as palavras do português brasileiro servem muito bem para dirimir ambiguidades na notação matemática.
(Mas é claro que, se combinar com seu leitor de outra forma, pode contar os algarismos da direita para a esquerda. Essa regra não está escrita em pedra.)
{4}/ Número e numeral: parte I
Um sujeito mostrou a C2h uma folha de papel A4 na qual desenhou uma bolinha vermelha, e lhe perguntou:
— Quantas bolinhas vermelhas há nesta folha?
C2h respondeu prontamente:
— Uma!
Em seguida, o sujeito mostrou outra folha A4 na qual desenhou dezenove bolinhas vermelhas, marcadas na página como que a esmo, e repetiu a pergunta.
Desta vez, C2h vacilou.
Todo mundo vacila. A maioria dos adultos consegue dizer, sem contar, se há três ou quatro bolinhas na folha de papel; mas, a partir daí, todo adulto alfabetizado de alguma forma conta — por exemplo, reúne mentalmente as bolinhas em grupos de quatro. Ou simplesmente conta mesmo, com a ajuda dos dedos e das palavras: “Uma, duas, três, quatro, …”
O estudante deve entender bem a diferença entre número inteiro não negativo e o numeral que usa para representar o número. C2h supôs uma pessoa que reuniu 73 pedrinhas: o número é quantidade de pedrinhas. Supôs também uma pessoa que fez 73 risquinhos num pedaço de osso: o número é a quantidade de risquinhos. Depois supôs uma pessoa que deu 73 passos: o número é a quantidade de passos. 73 é o numeral que usou para representar o número. Se tivesse usado os algarismos α, β, γ, δ, ε, ζ, η, θ, ι, κ, em vez de 73 teria escrito θδ.
Contudo, para saber que a pessoa deu 73 passos, C2h teve de contar, e para compreender bem essa ideia de representar uma contagem com dez símbolos, preparou a tabela 1 a seguir.
>> Tabela 1:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Com a ponta da caneta quieta sobre o algarismo 0, C2h pensou: “Ainda não dei nenhum passo. Zero passo até agora.” Depois, começando em zero, C2h deu oito passos, e anotou o algarismo sob a ponta da caneta quando parou: 8. Na figura 1 a seguir, cada asterisco representa um passo:
>> Fig. 1:
0 * 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8
Brincou assim mais algumas vezes. Com a ponta da caneta sobre 0, deu quatro passos, e anotou o algarismo sob a ponta da caneta: 4. Voltou para 0, deu sete passos, anotou 7; voltou para 0, deu um passo, anotou 1. Depois brincou dessa maneira um pouco mais. Queria consolidar bem a distinção entre número inteiro não negativo e o numeral que usa para representar o inteiro. Até que teve a ideia de brincar com as letras gregas: repousou a ponta da caneta em α e contou dois passos: anotou γ; depois voltou para α e contou nove passos: anotou κ.
Daí voltou a usar os algarismos hindu-arábicos e teve a ideia de dar 23 passos.
{5}/ Uma distinção necessária
Para pôr a ideia em prática, C2h desenhou uma grade de algarismos para ajudá-lo na contagem, que é a grade na tabela 2.
>> Tabela 2:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Manteve a ponta da caneta pairando sobre o primeiro zero, e então contou 23 passos; quando chegou ao 9 da primeira linha, passou para o 0 da segunda, e assim por diante. Por fim, anotou o numeral correspondente a vinte e três passos: 3.
— É óbvio que isso não vai funcionar, pois não dá para usar o numeral 3 para representar três passos, treze passos, ou vinte e três passos. Preciso achar um jeito de distinguir as linhas da tabela 2 entre si.
{6}/ Calculus (sing.), calculi (pl.)
Na antiguidade, muitos usaram alguma versão de ábaco para contar. Na Roma antiga, por exemplo, uma versão popular incluía pedrinhas (calculi) e uma caixa de areia com divisórias: uma pedrinha na divisória das unidades significava 1. Duas pedrinhas na divisória das centenas significava 200.
{7}/ O poder explicativo de uma tabela
Demorou um bocado para que o homem percebesse que não precisa de muitos símbolos para representar os inteiros não negativos, pois podia adaptar uma ideia que já estava presente no ábaco: use as mesmas pedrinhas, mas altere seu valor conforme a posição que ocupam. C2h lembrou-se disso e, em vez de inventar novos algarismos para distinguir três passos de treze passos, e treze passos de vinte e três passos, usou duas posições para representar cada número. “Tenho de manter a ideia básica”, pensou, “que é sempre usar os algarismos na mesma ordem: do menos significativo ao mais significativo, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.” Com esse propósito, montou a tabela 3.
>> Tabela 3:
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |
| 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 |
| 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 |
| 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 |
Mais uma vez C2h manteve a ponta da caneta sobre 00, querendo dizer “ainda não dei nenhum passo”, e depois contou três passos; voltou para 00 e contou treze passos; voltou para 00 e contou vinte e três passos. Desta vez, contudo, produziu três numerais distintos para cada número: 03, 13, 23.
Hung-Hsi Wu, pesquisador americano especializado em matemática elementar, professor na Universidade da Califórnia em Berkeley, diz que muita gente não chega a perceber o poder explicativo de tabelas como a 1, a 2, e a 3. C2h aceitou o desafio e tentou ver quantas explicações poderia bolar apenas movendo a ponta da caneta sobre os numerais da tabela 3.
(I) C2h repousou a caneta sobre a casa 00 e depois pulou para a casa 10, a 20, a 30, a 40. Escreveu no caderno: “Quando saltei de 00 para 10, é como se tivesse dado dez passos; quando saltei de 10 para 20, é como se tivesse dado mais dez passos; quando saltei de 20 para 30, é como se tivesse dados mais dez passos; e quando saltei de 30 para 40, é como se tivesse dado mais dez passos. Assim, saltar de 00 para 40 equivale a contar quarenta passos. Com o algarismo 1 em 10 eu digo que estou na segunda linha de numerais, e com isso digo que, pela primeira vez, estou usando os dez algarismos 0, 1, 2, …, 9 uma vez mais. Com o primeiro algarismo 4 em 40 eu digo que estou na quinta linha de numerais, e com isso digo que, pela quarta vez, estou usando os dez algarismos 0, 1, 2, …, 9 uma vez mais.”
(II) Seguindo uma indicação de Hung-Hsi Wu, C2h escreveu ainda: “Com o algarismo 7 em 74, eu indico a meu leitor que estou falando de um numeral que está na oitava linha da tabela 3. Meu leitor verá que deve contar sete linhas completamente antes de chegar a 70, e que portanto deve contar setenta passos de 00 a 70, mais quatro passos de 70 a 74. É por isso que o algarismo 7 em 74 vale setenta unidades, e o algarismo 4, quatro unidades.”
(III) Hung-Hsi Wu escreve em Understanding Numbers in Elementary School Mathematics: “Fazendo assim, o estudante vê que, quando coloca o algarismo 3 antes de 0, 1, 2, …, ou 9, quer dizer que já usou três vezes o conjunto de algarismos 0, 1, 2, …, 9, e por causa disso esse algarismo 3 não pode valer simplesmente três unidades.”
(IV) C2h passou a explorar a consequência natural dessas ideias: como ficaria uma tabela com numerais de três algarismos? (Ou de três dígitos.) Para responder à pergunta, montou a tabela 4.
>> Tabela 4:
| 000 | 001 | 002 | 003 | … | 099 |
| 100 | 101 | 102 | 103 | … | 199 |
| 200 | 201 | 202 | 203 | … | 299 |
| … | … | … | … | … | … |
| 900 | 901 | 902 | 903 | … | 999 |
Em outras palavras, C2h colocou todos os numerais da tabela 3 na primeira linha da tabela 4. Na segunda linha, com o algarismo 1 do numeral 100, indicou o fato de que 100 está na segunda linha, que já usou os cem numerais de 00 a 99 uma vez, e que portanto precisou de cem passos para partir de 000 e chegar a 100. Com o algarismo 2 de 203, indicou o fato de que 203 está na terceira linha e que, para partir de 000 e chegar a 200 teve de dar duzentos passos, e usar os cem numerais de 00 a 99 duas vezes. “Fica mais claro por que o algarismo 3 do numeral 356 significa a contagem de trezentos passos!”
{8}/ O sistema binário
C2h quis saber: “E se, em vez de dez algarismos, eu tivesse só dois, 0 e 1, nessa ordem? Poderia manter o controle sobre o número de passos?”
Com os algarismos 0, 1, montou mais uma tabela de contagem, a tabela 5.
>> Tabela 5:
| 0 | 1 |
Pôs a ponta da caneta sobre o zero e quis contar dois passos. Não deu. “Com só dois algarismos e numerais de uma posição, só posso registrar dois números, os números equivalentes a contar nenhum passo ou contar um passo.” Para reusar os dois algarismos, montou a tabela 6, com numerais de duas posições.
>> Tabela 6:
| 00 | 01 |
| 10 | 11 |
C2h viu que agora pode contar até três passos. Se não contar nada, marca 00. Se contar um passo, marca 01. Se contar dois passos, marca 10. E se contar três passos, marca 11. Viu também que, se põe a ponta da caneta em 00, e depois disso pula para 10, é como se tivesse dado um pulo de dois passos. “Sempre que o algarismo na primeira posição muda de 0 para 1”, escreveu C2h no caderno, “é como se eu tivesse andado mais dois passos a partir do numeral anterior.”
E, logo depois desses pensamentos, montou a tabela 7, com numerais de três posições, que lhe permitiriam reusar os numerais de dois algarismos duas vezes.
>> Tabela 7:
| 000 | 001 | 010 | 011 |
| 100 | 101 | 110 | 111 |
Partindo de 000, C2h contou cinco passos, e registrou a contagem com 101. Voltou para 000 e contou sete passos: 111. “Com dois algarismos e três posições, tenho oito numerais distintos, com os quais posso contar de zero passo a sete passos.” Não deixou de notar que 2 × 3 = 8. Viu também que, se pula de 000 para 100, dá um salto equivalente a quatro passos. E mais uma vez montou uma tabela 8 para ver os numerais de quatro posições e dois algarismos.
>> Tabela 8:
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
C2h explorou as semelhanças com o que já vinha fazendo, a começar pelo nome:
[1] O sistema numérico da tabela 8 é um sistema numérico posicional binário hindu-arábico.
[2] O número não muda, pois está vendo “número” como “quantidade de passos”. O que muda é o numeral com o qual representa cada número.
[3] Com dez algarismos e duas posições, C2h pode atribuir um numeral distinto para cem inteiros não negativos (10 × 10 = 100), que são os inteiros de 00 a 99. Com dois algarismos e duas posições, pode atribuir um numeral distinto para quatro inteiros não negativos (2 × 2 = 4).
[4] Quando usa a base 10 e escreve 23, quer dizer com o algarismo 2 que já usou os dez algarismos duas vezes ao partir de 00 para chegar a 20, isto é, que deu vinte passos da casa 00 à casa 20. Quando usa a base 2 e escreve 11, quer dizer com o primeiro algarismo 1 que já usou os dois algarismos uma vez ao partir de 00 para chegar a 10.
[5] No sistema binário, quando salta de 0 para 1, dá um salto de um passo (20); quando salta de 00 para 10, dá um salto de dois passos (21); quando salta de 000 para 100, dá um salto de quatro passos (22); quando salta de 0000 para 1000, dá um salto de oito passos (23); e assim por diante.
[6] Ao escrever 1111 no sistema binário, C2h passa a seguinte mensagem a seu leitor: “Com o primeiro algarismo 1, quero dizer que contei oito passos de 0000 a 1000, e por isso usei uma vez todas as permutações de dois algarismos em três posições; com o segundo algarismo 1, quero dizer que contei quatro passos de 000 a 100, e por isso usei uma vez todas as permutações de dois algarismos em duas posições; com o terceiro algarismo 1, quero dizer que contei dois passos de 00 a 10, e por isso usei uma vez todas as permutações de dois algarismos em uma posição; com o quatro algarismo 1, quero dizer que contei um passo de 0 a 1.” C2h notou que 1111 na base 2 vale 15 na base 10, e que, na base 10, 8 + 4 + 2 + 1 = 15.
{9}/ A presença de Deus
Gottfried Wilhelm Leibniz (1646-1716), matemático alemão, um dos inventores do cálculo diferencial e integral, foi também o primeiro matemático a descobrir que podia denotar qualquer inteiro não negativo com somente dois algarismos, 0 e 1. Ele ficou profundamente impressionado com a descoberta, e viu nela uma evidência da presença de Deus. Chegou a mandar uma carta para missionários cristãos na China, explicando sua descoberta em detalhes, na esperança de que os missionários pudessem recorrer ao sistema numérico posicional binário para converter mais chineses ao cristianismo.
{10}/ A ciência dos saltos
Olhando as tabelas 3 e 4, C2h notou uma propriedade interessante: começando em 0, se dá dez saltos de 10 unidades, chega a 100. Assim: 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Começando em 0, se dá dez saltos de 100 unidades, chega a 1.000: 0, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1.000. Começando em 0, se dá dez saltos de 1.000 unidades, chega a 10.000: 0, 1.000, 2.000, 3.000, 4.000, 5.000, 6.000, 7.000, 8.000, 9.000, 10.000. Como poderia expressar essa descoberta? Escreveu assim: “Seja n um número inteiro positivo. Se eu começo na casa 0 e conto em saltos de 1000…0 (1 seguido de n zeros), daí, depois de dez saltos, chego à casa 1000…0 (1 seguido de n + 1 zeros).”
Eis como C2h desenhou o que está querendo dizer:
É uma observação útil para usar com a definição de adição e a de multiplicação de inteiros não negativos.
(“Formulário” significa “conjunto de fórmulas”.)
{11}/ O conceito de adição
Com o que já descobriu até aqui, C2h se sentiu capaz de definir o conceito de adição só com a ajuda das tabelas de contagem, especialmente a tabela 3.
“Quero agora definir a adição de quatro passos com cinco passos”, escreveu no caderno. “Para denotar essa operação de adição, vou usar a expressão 4 + 5. Quero dizer com ela o seguinte: 4 + 5 representa o inteiro não negativo que obtenho ao deixar a ponta da caneta pausada sobre o numeral 4, e então contar mais cinco passos a partir de 4.” Para deixar mais claro o que quis dizer, produziu a figura 2.
>> Fig. 2:
| 00 | 01 | 02 | 03 | 04 | |||||
| 00 | 01 | 02 | 03 | 04 | 05 | ||||
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 |
| 00 | 01 | 02 | 03 | 04 | 05 | ||||
| 00 | 01 | 02 | 03 | 04 |
Como ao contar cinco passos a partir de 04 ficou com a ponta da caneta sobre o numeral 09, então pôde usar o sinal “=” para expressar o fato de que, na equação mais abaixo (no formulário 2), a expressão 4 + 5 equivale a 9, isto é, de que contar cinco passos a partir da casa com o numeral 04 equivale a contar nove passos a partir da casa com o numeral 00. De quebra, com a figura 2, achou bem fácil acreditar também que 4 + 5 = 5 + 4, isto é, que a adição é comutativa.
“De modo mais simples e mais geral”, escreveu, “se estou trabalhando com inteiros não negativos, posso dizer que a soma a + b é o inteiro c que obtenho ao contar b passos começando em a, e posso contar essa história escrevendo a + b = c ou c = a + b. Agora, quando escrevo a + b + d, quero dizer o inteiro que obtenho ao contar d passos a partir de a + b; é claro que isso é a mesma coisa que c + d.” A partir desse ponto, e ainda olhando a tabela 3, C2h chegou à conclusão de que 9 + 3 = 3 + 9 = 4 + 5 + 3 = 3 + 4 + 5 = 5 + 4 + 3 = 3 + 5 + 4 = 12, e disso tudo, mais genericamente, que a + b + c + ··· + n = n + ··· + c + b + a, onde tais letras denotam inteiros não negativos.
{12}/ A ideia de “vezes”
Com a definição de adição, C2h voltou à ideia dos saltos. Se começa em zero e dá dez saltos de dez passos por vez para chegar a 100, pode dizer que começou em 10 e deu nove saltos de dez passos para chegar a 100. Ao contar essa história com notação matemática, escreveu:
C2h fez mais uns testes com afirmações semelhantes (testou 1.000, 10.000, 100.000), e daí chegou a uma afirmação mais genérica: “Se uso n para denotar um inteiro positivo, daí posso escrever tais afirmações de modo mais genérico.” Eis o que produziu:
{13}/ A forma expandida
Com tudo isso, C2h viu que, quando escreve 5.725, com o primeiro algarismo 5, quer dizer 5.000 passos a partir do zero; com o segundo algarismo 7, quer dizer mais 700 passos a partir do numeral 5.000; com o terceiro algarismo 2, quer dizer 20 passos a partir do numeral 5.700; e com o quarto e último algarismo 5, quer dizer 5 passos a partir do numeral 5.720. Como contar essa história com as definições que já tem até aqui?
C2h descobriu que pode chamar a soma 5.000 + 700 + 20 + 5 de “a forma expandida de 5.725”.
{14}/ Maior, menor
Com esse jeito de olhar os números inteiros não negativos e os numerais que usa para representá-los, C2h notou que fica fácil representar a ideia de que um número é menor ou maior que outro: no processo de contagem, se o inteiro a ocorre primeiro que o inteiro b, então a é menor que b (ou b é maior que a). Escreveu isso em símbolos:
Lendo sobre o assunto, descobriu algo que pouca gente sabe: que pode expressar ambas as linhas com as mesmas palavras. Se quiser, ou se achar necessário, pode escrever b > a e dizer as palavras “a é menor que b”; ou pode escrever a < b e dizer “b é maior que a”.
C2h escreveu no caderno: “Se estou comparando dois inteiros, como posso traduzir o fato de que ou os dois são iguais, ou um é maior que o outro, ou um é menor que o outro?” Para guiar o pensamento, usou como exemplos os números 3.765 e 3.755. “Fica claro que devo comparar os numerais posição a posição, algarismo a algarismo. Se o primeiro algarismo dos dois é o mesmo, neste caso 3, significa que nos dois casos precisei contar três mil passos da casa 0.000 à casa 3.000, e nos dois casos a ponta da minha caneta está sobre a casa 3.000. Se o segundo algarismo dos dois é igual a 7, significa que, a partir da casa 3.000, nos dois casos precisei contar mais setecentos passos, e a ponta da minha caneta nos dois casos está sobre a casa 3.700. Agora, no primeiro caso, contei sessenta passos a partir da casa 3.700, e no segundo caso, contei cinquenta passos. No primeiro caso, a ponta de minha caneta parou sobre a casa 3.760. No segundo, sobre a casa 3.750. Fui mais longe no primeiro caso, e por isso 3.765 é maior que 3.755, ou 3.755 é menor que 3.765”
Se estivesse comparando dois inteiros com número distinto de algarismos, C2h viu que, para usar o raciocínio acima, bastaria completar um dos numerais com zeros à esquerda. Por exemplo, para comparar 3.765 com 833, basta adicionar um zero à esquerda de 833 e comparar 3.765 com 0.833. “3.765 é maior que 0.833 porque, no primeiro caso, precisei contar três mil passos de 0.000 até 3.000. Repeti três vezes meu conjunto de numerais de três algarismos. No segundo caso, não saí do lugar: a ponta da caneta permaneceu imóvel sobre a casa 0.000.” Essa ideia dá ensejo a um algoritmo bacana, e C2h o colocou no papel:
“Suponha que eu esteja comparando dois inteiros não negativos com a mesma quantidade de algarismos. Indo da esquerda para a direita, comparo os dois inteiros, posição por posição, algarismo por algarismo, até que chego a uma posição na qual os dois algarismos diferem. Posso declarar como sendo maior o inteiro cujo algarismo, nessa posição, é maior. Se os dois inteiros não têm a mesma quantidade de algarismos, posso imediatamente declarar como sendo menor aquele que precisei preencher com zeros à esquerda.”
{15}/ Tricotomia
Depois de associar a ideia de número com a de passos, e de dissociar a quantidade de passos do modo como registra a quantidade de passos (o numeral), em pouco tempo C2h entendeu perfeitamente por que ou dois inteiros não negativos a e b são iguais (a = b), ou um é maior que o outro (a > b), ou um é menor que o outro (a < b). Muito adulto acha natural esse axioma da tricotomia, mas não sabe explicá-lo adequadamente.
{16}/ Número e numeral: parte II
C2h tomou cuidado para distinguir número de numeral. Em alguns textos, como este, tal distinção é importante. Na maioria das situações cotidianas, porém, não há nenhum problema em chamar 275 de número. Mas C2h sabe que, de vez em quando, deve trazer tal distinção à mente e brincar com ela.
Por exemplo, o número quinze é um número ímpar; C2h não consegue dividir quinze passos em dois grupos com a mesma quantidade de passos, pois um dos dois grupos sempre fica com um passo a mais. Quinze sempre será um número ímpar, mesmo quando C2h o registra com o sistema posicional hindu-arábico de base 5, no qual monta os numerais apenas com os algarismos 0, 1, 2, 3, 4 e no qual deve grafar “quinze passos” com o numeral 30. A propriedade de ser par ou ímpar é uma propriedade do número, e não do numeral. O fato de que os numerais de base 10 terminados em zero são pares é mera coincidência.

Em certos sistemas numéricos posicionais, como o de base 5, números pares e ímpares terminam em zero
{17}/ A multiplicação de inteiros
Na vida de quem adiciona inteiros não negativos, ocorre com frequência a necessidade de adicionar um monte de parcelas idênticas, como 5 + 5 + 5 + 5 ou 76 + 76 + 76. C2h sabe que existe um jeito mais fácil de grafar casos assim:
>> Formulário 7:
Com o símbolo de igual com uma bolinha em cima, C2h quis dizer: “Eu defino o significado da expressão à esquerda, que por enquanto meu leitor desconhece, com o significado da expressão à direita, que meu leitor já conhece.” Uma vez que a definição esteja pronta, ninguém precisa mais repetir esse símbolo: basta usar o sinal de igual comum.
Lendo sobre o assunto, C2h descobriu que não deve dizer: “A multiplicação de inteiros não negativos é uma adição de parcelas repetidas.” Na verdade, o conceito de multiplicação é distinto do conceito de adição, mas, no caso de inteiros não negativos, os dois conceitos se complementam perfeitamente bem. (Resumindo bastante, a história transcorreu assim: antigamente, os matemáticos definiram a multiplicação como sendo uma adição de parcelas repetidas; depois, conforme aprenderam mais, descobriram muitas situações nas quais essa definição não faz sentido, como na multiplicação de matrizes, e hoje sabem que cada uma das duas operações merece lugar de destaque uma ao lado da outra. Elas têm a mesma estatura.) C2h achou um jeito interessante de expressar com palavras as expressões no formulário 7: “Quando eu julgar conveniente, posso ver uma adição repetida de inteiros não negativos como se fosse uma multiplicação de dois inteiros não negativos, e vice-versa, desde que não me esqueça de que nem sempre posso ver a multiplicação como sendo uma adição repetida.”
Eis um jeito mais genérico de usar a ideia de multiplicação para simplificar a notação da adição repetida de inteiros não negativos:
Pode chamar n e x de fatores, e pode chamar nx (o resultado da multiplicação de n por x) de produto.
C2h já conhece bem muitos aspectos da multiplicação e da adição de números reais, mas tentou ver o que conseguia deduzir sobre tais operações com inteiros não negativos apenas com as definições desta matéria. Viu que pode fazer muita coisa:
a) A multiplicação de inteiros não negativos é comutativa: nx = xn.
b) Como atribuir significado a 3 · 5 · 8? “Por exemplo”, escreveu C2h, “faço 3 · 5, isto é, 5 + 5 + 5: começo na casa 00 e conto cinco passos para chegar à casa 05; a partir dessa casa, conto mais cinco passos para chegar à casa 10; e a partir dessa casa, conto mais cinco passos para chegar à casa 15. E então, usando a mesma receita, faço 15 · 8 = 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 = 120.”
c) Olhando as expressões na seção 11, C2h viu que poderia escrever assim, se quisesse:
Assim, 10 · 10 = 100; 10 · 100 = 1.000; 10 · 1.000 = 10.000; etc. Substituindo uma fórmula na outra:
Brincando com mais alguns exemplos, não achou difícil concluir que o número de zeros depois de 1 é igual ao número de fatores iguais a 10, isto é:
Ele já sabia que matemáticos escrevem 10 como 101, 100 como 102, 1.000 como 103, 10.000 como 104 e, mais genericamente:
C2h achou fácil usar só o que sabe até aqui para deduzir uma lei muito útil:
E com isso, sempre recorrendo apenas a definições simples, pôde redefinir a igualdade no formulário 11 (os três pontinhos em triângulo significam “portanto”):
Logo depois, pensou no significado de 100, já que, por enquanto, está lidando com inteiros não negativos e o zero é um inteiro não negativo. Experimentou várias possibilidades, e por fim montou uma lista.
“Ora”, escreveu, “105 é 104 vezes 10; 104 é 103 vezes 10; 103 é 102 vezes 10; 102 é 101 vezes 10. Para manter essa lista consistente, devo dizer que 101 é 100 vezes 10, o que me obriga a declarar 100 = 1.” E foi o que fez.
“Quando leio 10n”, escreveu C2h, “devo dizer ‘dez elevado à enésima potência’ ou ‘dez elevado ao expoente n’. Por exemplo, com 105, devo dizer ‘dez elevado à quinta potência’ ou ‘dez elevado ao expoente cinco’.”
Mais uma vez, C2h notou que deve fazer distinção entre a operação de potenciação e a de multiplicação. São duas operações distintas, de mesma estatura, sendo que os matemáticos chamam a operação de potenciação de “operação analítica”, pois, com frequência, só pode ser adequadamente definida com a ajuda do cálculo diferencial e integral, muitas vezes com a ajuda de séries infinitas (somatórios com número infinito de parcelas). É o caso de da expressão ei√2, na qual e é uma constante, i é a unidade imaginária, e √2 é o número real que, multiplicado por si mesmo, resulta em 2. Contudo, nas operações aritméticas básicas, que C2h realiza com inteiros não negativos, se quiser pode ver a multiplicação de fatores repetidos como se fosse uma potenciação de expoente não negativo, e vice-versa.
{18}/ Voltando ao começo
Com tudo isso, C2h viu que estava pronto para definir a ideia de sistema posicional decimal hindu-arábico do modo como os matemáticos o definem, com a diferença de que, desta vez, domina cada passo da definição.
Começou notando que 4.000 = 4 · 1.000; 300 = 3 · 100; 70.000 = 7 · 10.000. Desse modo, pensando em p como um dos algarismos 0, 1, 2, 3, …, 9:
Assim, 4.000 = 4 · 103, 300 = 3 · 102, 70.000 = 7 · 104, etc. O algarismo 4 em 4 · 103, o algarismo 3 em 3 · 102, e o algarismo 7 em 7 · 104 se chamam coeficientes: em 7 · 104, C2h pode dizer, se quiser: “sete é o coeficiente de dez elevado ao expoente quatro” ou “sete é o coeficiente da quarta potência de dez”.
Então, qual é a forma expandida de 540.077.504? Ela é:
>> Formulário 18:
C2h até pensou numa cola com a qual pode montar somatórios como o do formulário 18 sem cometer nenhum erro, e foi assim que montou a tabela 9.
>> Tabela 9:
| 5 | 4 | 0. | 0 | 7 | 7. | 5 | 0 | 4 |
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Na linha de cima, estão os algarismos do numeral a converter no somatório da forma expandida; na linha de baixo, os expoentes de 10. Uma tabela assim deixa claro por que, ao acrescentar zeros à esquerda de um numeral, C2h não altera seu valor: ora, 0 · 10n é igual a zero para qualquer valor de n.
“No mundo da educação matemática”, diz Hung-Hsi Wu, o especialista de Harvard, “às vezes a expressão ‘saber algo’ significa, na verdade, ‘decorar algo’. Uma pessoa diz que 7 vezes 8 vale 56: talvez saiba o que está dizendo, ou talvez tenha decorado o resultado. Então, quando o matemático usa a expressão ‘saber algo’, quer dizer algo completamente diferente: na matemática, se o matemático diz que conhece um conceito, ele conhece a definição precisa, conhece o conceito intuitivamente, sabe por que ele é verdadeiro, sabe por que vale a pena conhecê-lo, sabe quando pode usá-lo, sabe o contexto natural no qual o conceito aparece. Enfim, sabe a história completa.” {FIM}
* * *
Aviso: Se gostou deste texto e se lê inglês, compre o livro Understanding Numbers in Elementary School Mathematics, de Hung-Hsi Wu. É um livro extraordinário. Em todo caso, pretendo continuar usando o livro de Wu como ponto de partida para textos sobre aritmética elementar, como fiz com este texto. Não perca!














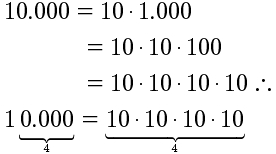



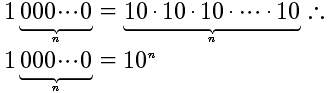
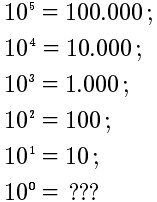



muito bom! posso usa em minhas aulas?!… Math é pura magia…
CurtirCurtir
Sim, é claro que pode. Não deixe de ler o livro de Hung-Hsi Wu, que menciono na matéria, pois é muito bom. Abraço!
CurtirCurtir